The economic dimension of public-private partnership in transport

Vincent Piron
Strategy Vice President for VINCI Concessions

“The primary advantage of economics is its educational role. Building and discussing a model, however imperfect, are not fruitless tasks. They are for the business man what Kriegspiel is for the military man.”

Pierre Massé
Former French national planning commissioner

Introduction

All too often, discussions, lectures, seminars and the various congresses devoted to public- private partnerships focus on points of judicial or legal procedure, or conversely, on doctrinal positions on public service that confuse responsibility for the organisation of a service with the actual provision of that same service. The economic aspect has been very much ignored, with attention being concentrated on the financial and budgetary dimension of the topic. Nevertheless, the fact that a project is viable in economic terms does not mean it can be funded, and conversely, the fact that a legal procedure exists for funding a project does not mean that it is economically worthwhile and that it should therefore be implemented.

In the present article, with the valuable assistance of Professor Rémy Prud’homme, Claude Abraham, the Forecasting Directorate at the French Ministry of Finance (J. J. Becker and C. Audenis), the Conseil Général des Ponts et Chaussées (French General Council for Road and Bridge Engineering) (Alain Bernard) and Olivier Piron (former permanent secretary to the national planning body for urban development, construction and architecture), we have built an economic and financial model in order to contribute to the effort to include the classic calculations of economics among the parameters that managers might consider when working toward decisions as to whether or not to proceed with a construction project. Our remarks will address the area of toll infrastructures, and more precisely a case that, while theoretical, is closely modelled on that of the Rion-Antirion Bridge, which Vinci constructed and financed in Greece under a 40-year concession agreement. Public-private partnerships can be applied in many other areas, especially for the construction of buildings or the provision of services, but the economic model we set out to describe below is designed for a process involving the design, funding, construction and operation of a transport infrastructure for which a toll is charged.

At a time when the dual question of the definition (the State as actor or as regulator) and the effectiveness (a State changing at the rate required by international competition or a State governed by rules dating back decades) of the role of the State is a topical one, it seemed to us to be useful to apply laws already familiar in economics and finance to a concrete case in order to measure their impact and thus help decision-makers and private partners reach judicious decisions.

We will make use of data and concepts already presented in our previous articles, especially the papers describing the concept of bitterness (Transports issues 402 and 408), and the economic efficiency and the budgetary dimension of the Prado-Carénage tunnel in Marseilles (Transports issue 416).

Positioning the problem

The principles of calculation in economics: utility and resources

Utility can be calculated

If local government decides to invest money it has collected through taxes in a construction it is because that construction has a certain utility for the community. A hospital, a road, a swimming pool, a police station, all have utility for the community. And utility is a quantity that can be measured, and is also known as “socio-economic benefit”, or “surplus” according to Jules Dupuit 1. Although measurable in principle, and despite the fact that the concept has been formally established for nearly two hundred years, the economic utility generated by a construction is generally difficult to quantify and is often replaced by an “intuitive and political” assessment of the necessity of investing, which is combined with the constraint imposed by the limited availability of public funds.

In the pages which follow, we define “utility” as the net balance of socio-economic benefits (sometimes called “positive externalities”) after deduction of negative externalities such as pollution, noise, etc. In the area of transport, the largest component of utility is currently considered to derive from the time saved by users, the value of which is determined by the value of time. Thanks to the construction of infrastructures for which a toll is charged and to the new information technologies, this can now be more effectively defined.

In sectors other than transport – health, education or justice, for example – the quantification of utility is more problematic, public decision-makers do not always have the right tools to hand, and budgetary constraints are all too often used as the sole criterion for screening decisions. There are a small number of global studies by the World Bank on teaching and health. We are also beginning to have the benefit of a few quantified experiments in schools, naturally in the United States and the United Kingdom, whose lead in the sphere of economic studies needs, unfortunately, no further demonstration!

In France, the evaluations conducted under the French domestic transport reform law (LOTI ) have not received the attention that the subject deserves, and even flagship projects such as the Lyons northern bypass, which caused much ink to be spilt on legal and purely political matters, has never, to our knowledge, been subjected to any comprehensive profit and loss assessment. This is a pity because the few figures that we have been able to estimate in order to evaluate the utility of this infrastructure indicate that the net outcome of the project is very positive – on the basis of its current toll pricing, naturally.

The discounted value of resources deployed and socio-economic benefits generated

Construction resources are mobilised for periods of a few months, but socio-economic benefits are generated year after year throughout the lifetime of the infrastructure. In order to express values that are spread over a long period in terms of the current year in which the decision is taken, a discount rate ‘τ’ is applied, which involves dividing each value for resources or utility by a factor equal to (1+τ)^t, as is done when calculating IRR. The resulting figure is called the “net present value” (NPV) which is the sum of all the values expressed in terms of the initial year.

NPV of mobilised resources = ΣtCt*1/(1+τ)t NPV of utility = ΣtUt*1/(1+τ)t

1
Jules Dupuit was one of the founders of modern economics. His key concepts date from 1844 and 1849. 2
In the model, in order to compare the various solutions from the economic standpoint, we shall make use of the NPV of the various quantities considered. For the purposes of clarity, we have used the quantified example of a government authority wishing to carry out a construction at an overall cost of €30m, to be spread over three years, and whose annual operating costs will be equal to 2% of the investment.

Graph 1 below relates the minimum utility to be obtained to justify the construction project to the discounted rate for the public authority concerned. The computation is done by balancing the NPV of the mobilised resources with the NPV of the project’s utility. For example, at a rate of 8%, a minimum annual utility of €3.25m is needed to justify the overall investment of €30m 2.

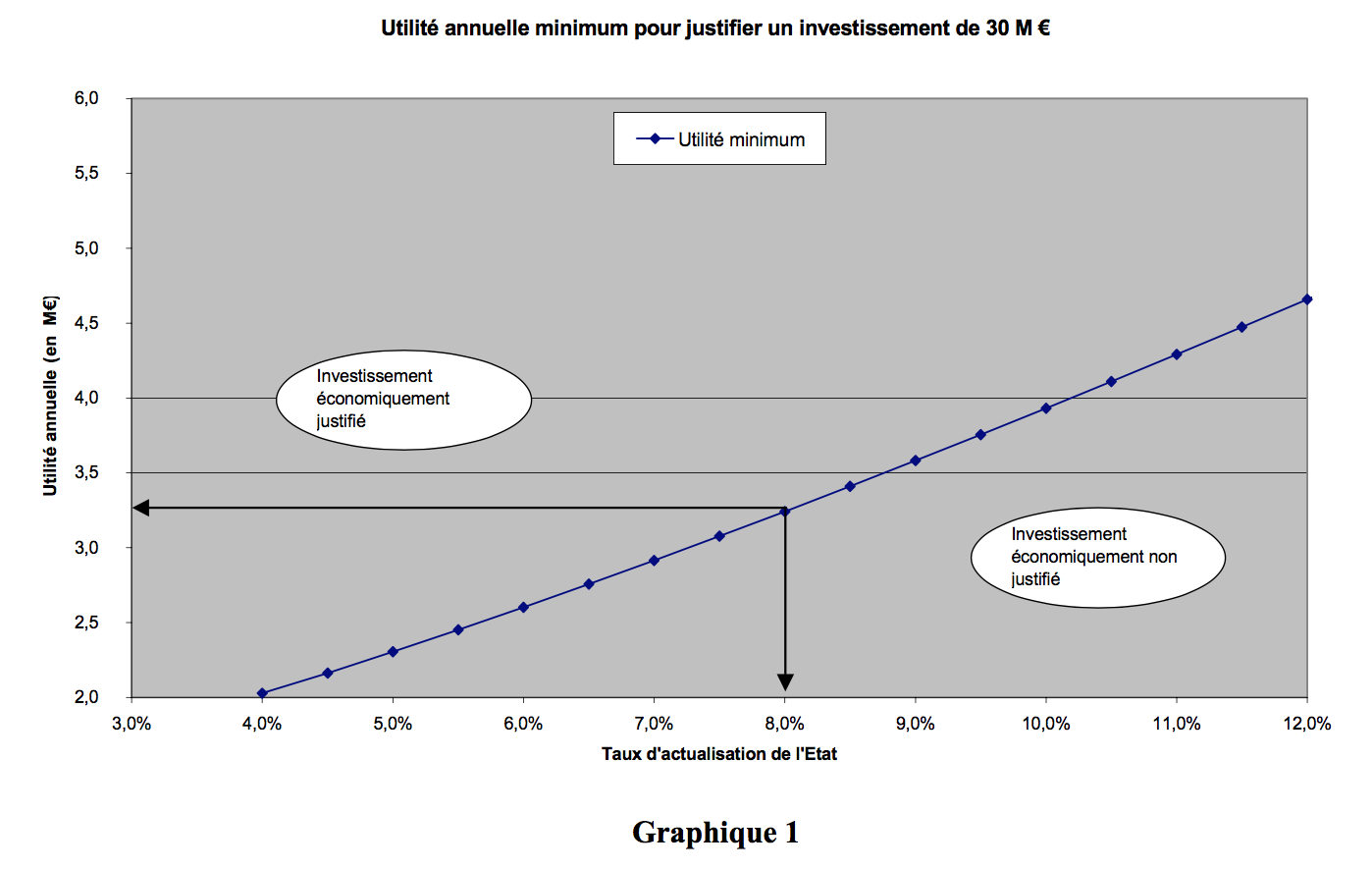
But what discount rate should be applied in order to define the construction projects to be carried out and what about the funding indispensable to their execution?

We can quote the Forecasting Directorate. “Since 1985, the National Planning Commission has recommended the use of a discount rate for public investment of 8% in constant monetary terms. However, at the present time a number of studies no longer support that figure, as is the case for the Charpin-Dessus-Pellat report 3, which recently opted for a rate of 6%. Lower interest rates and a growing awareness of the need to preserve the environment for future generations are the main factors put forward to explain the use of discount rates lower than those recommended in the past. Conversely, the observation that higher rates are applied by private enterprise argues in favour of raising the public discount rate in order to avoid introducing a gap between the private and public sectors. Economic theory may provide a framework for the assessment of the worth of these arguments, as well as an order of magnitude for a satisfactory rate” 4.

Countries with comfortable public finances which pay attention to the long-term future will work with discount rates in the region of 4% to 6% in real terms. At the other end of the spectrum,

IRR and NPV calculations are easily carried out using the financial functions of spreadsheets. Prospective economic analysis of the nuclear energy production sector.
Internal Forecasting Directorate memorandum on discount rates (MM XXX).

Annual utility (€ millions)
developing countries frequently use a rate of 12%, in accordance with the practices recommended by the World Bank in its economic analyses. France’s official rate has been 8% for several decades, but it is currently considered by many experts (the French national planning commission, the Ministry of finance, the Ministry of national infrastructures) as too high by approximately 2%. Finally, we have chosen to apply a figure of 6% for all economic computations.

Socio-Economic Internal Rate of Return and Discount Rate

Internal Rate of Return is defined as the rate at which the discounted sum of the costs balances the discounted sum of the socio-economic benefits over the lifetime of the construction. It is calculated using values C and U as follows:

ΣtCt*1/(1+r)t = ΣtUt*1/(1+r)t
Where:
C is the annual amount of the investment up to the entry into service of the construction.
U is net utility (gross utility less negative externalities, maintenance costs and operating expenses). t varies from 1 at the end of the period of use of the construction (55 years in our model).
r is the internal rate of return for the construction: IRR(SE).

Economic theory indicates that it will be advantageous for a government to implement a construction project if the IRR(SE) for the resulting infrastructure is greater than the government’s discount rate, a consideration that holds true irrespective of the arrangements whereby the project is funded.

For example, on this criterion the recent Van Miert report 5 on investment in transport in Europe sets the investment needed over the next ten years at a figure of €200bn. But the question of how this should be funded remains entirely open.

Opportunity costs (or marginal costs) of public funds

On this fundamental and thorny subject, we shall quote Alain Bernard 6, a member of the Conseil Général des Ponts et Chaussées:

The true cost of taxation, its economic cost, is that which derives from the distortions it entails. Economists are now well aware that the neutral taxation they had imagined – lump-sum transfers – was no more than an artefact. Every real-world fiscal system generates distortion – and it is obviously desirable that those systems should be optimised in order to generate – at a given level of tax revenue and for given redistribution objectives – the lowest possible distortion cost. This is the aim of the optimum tax theory, the nature of which is identical to optimum toll theory (in which Marcel Boiteux was the true pioneer).

The practical upshot of all the above is as follows: if one extra euro (from a given initial base) is raised in tax, the loss of well-being of consumers will be equivalent not to one euro of consumption but to (1+x) euros. The quantity (1+x) expresses the marginal cost of public funds.

The European Commission’s Van Miert report on transport infrastructures.
Cf. Alain Bernard and Marc Vielle, 2002. “Measuring the Welfare Cost of Climate Change Policy” and the report “Calcul économique et planification” [Economic computation and planning] published by Documentation Française in 1972.
It would, given this, be unreasonable to spend one euro of public funds to produce goods whose value to consumers was not at least equal to (1+x). It is therefore necessary, in economic calculations, to apply this adjustment factor to every item of expenditure funded from taxation. Conversely, every item of extra tax revenue generated by investment, for example by the domestic tax on petroleum products [TIPP] where investment in road systems is concerned, must be incremented by application of this same adjustment factor.

In 1984, the French national planning commission recommended that an adjustment factor of 1.5 should be adopted, while one study recently estimated that the marginal cost of public funds was 0.13 for France, which gives a factor of 1.13 7. However, the latter study is already a few years old and recent developments in the situation in France lead its author to feel that the figure should be significantly higher today. Following some discussion with the experts quoted above, and given the current constraints and high level of tax rates, this adjustment factor, which will be called the opportunity cost factor, will be set at a current value of 1.2.

In practical terms, this means that an investment of €100m must be entered as a cost of €120m in economic calculations, although that investment will still only be €100m in terms of budget calculations. The extra cost of €20m will be termed the “opportunity cost” in the pages which follow.

It does however seem to us to be both important and urgent for economists (public authorities and private sector) to look more closely at this subject since it has a direct and essential impact on the effectiveness of public decisions.

Valuing future budget flows over time

Conventional economic computations have an important feature: they take no account of the actual availability of funds, since they assume that those funds are always available and ready to finance an operation whose socio-economic IRR(SE) – is greater than the government authority’s discount rate.

The reality of the constraints imposed by budgets and public debt is quite another matter: the task is to work toward an optimisation of socio-economic benefits for the nation within budgetary constraints. Once the decision to go ahead with a construction project has been taken, in order to choose from among the resources available to complete it (public tender, concession, partnership agreements), the owner of the project will need to compare the series of monetary (budgetary) flows as planned from year to year over a long period for each of the possible solutions.

In order to do this, the decision-maker will need to select a discount rate that reflects the scarcity of public funds for budgets, that is to say the extent of the State’s “financial shortfall”. The tighter the constraints on the State, notably in terms of its debt and an already high level of mandatory levies (tax and sundry other dues), the more problems it will have as a consequence in raising funds, and the higher that rate must be. A “constraint-free” State would have a rate of 3%, and a State that is highly constrained would have a much higher rate, which theoretically could even be infinite if there were no public funds at all. The rate of 3% is the rounded figure for the current 10-year “swapped EURIBOR” rate, less inflation, since our calculations are in constant euros.

In the English-speaking countries and the Netherlands, which are much less constrained by the problems of debt with which we are familiar in France, the discount rate applied to budget expenditure in nominal value terms is set in some cases at 5% and in others at 6%.

In our model, we have selected the figure of 5%, but we have done a limited number of sensitivity tests by varying the rate between 3% and 8%, which do no modify the conclusions reached in the present article.

The various possibilities for the execution and funding of construction projects

Let us imagine that we are to build a bridge like the Rion-Antirion bridge being constructed at the present time by the Vinci group in Greece, in the north-western Peloponnese, in order to connect Patras to the Greek mainland. The questions of what options are available to a government to carry out such a project, and how their suitability can be judged – these are the issues we set out to examine below.

The various possible options for executing the project

The economic analysis necessary to determine whether a transport infrastructure should or should not be constructed is usually carried out without the knowledge of the future builder or operator, and even in ignorance of the future mode of funding. However, it is possible to demonstrate that the financial and institutional context has a direct bearing on the economic viability of a project, as well as, of course, on public budgets.

A number of options are open to decision-makers:
Option no. 1: the bridge can be constructed entirely from public funds as budgeted, and can then be thrown open to traffic without charge. It will be managed by a public entity ;
Option no. 2: at the opposite end of the administrative spectrum for the award of public contracts, it is possible to build a bridge entirely out of private funds, operated by a private company which derives its remuneration from the tolls collected. This is the classic case of a public infrastructure built under a concession agreement. In this case, the amount of the toll is discussed with the public authorities and must be set at a satisfactory level of political acceptability (cf. our studies published previously in the journal Transports). The revenue may be sufficient to cover operating costs, to repay the loans taken out with financial institutions and, lastly, to provide a reasonable return on the capital invested by the private enterprise. This state of affairs is increasingly rare, and occurs when a government has almost finished building a network and just one link remains to be built for it to be complete (as was the case for the Millau viaduct, for example) ;
Option no. 3: the bridge can be built by a public authority out of budget resources, with the imposition of a toll charged to users for the right to cross it. Toll revenue is paid into the general State budget ;
Option no. 4: a public establishment is specifically set up with the power to borrow money, construct the bridge and collect the revenue, which is then used to repay the loans. The economic and budgetary consequences of this, although similar, are not totally identical ;
Option no. 5: the State can decide to entrust responsibility for the construction (execution and operation) to a private company, even if a subsidy may be needed for the latter if the toll revenue is not sufficient to pay for the whole project ;
Option no. 6: the State can also entrust the building of the bridge to a private company, which will be remunerated in accordance with the traffic crossing it, but without users being charged a toll at point of use. The sums received by the enterprise will come from the State’s budget. This method of remuneration is known as a “shadow toll” in the English-speaking world ;
Option no. 7: Unfortunately, it must be noted that there is a seventh option, which is to do nothing in the immediate future; we shall take this into account in the present article by considering simply that the construction is put back by three years.
The economic analysis of these various processes of construction will be based on an examination of two indicators: the socio-economic internal rate of return and the net present value of the costs and benefits associated with the construction and operation of the facility. The socio-economic internal rate of return is the rate at which the net present value of the costs equals the net present value of the benefits.

The budget analysis will be carried out in terms of the general State budget, applying a discount rate of 5% to flows of expenditure and revenue.

Determination of parameters

For this same bridge, the various options for structuring the project lead to different results in each case. This is because there are four major quantities to be taken into account: the total cost of the construction, the opportunity cost for public funds, and the financial revenue deriving from the activity generated by the completed construction.

Socio-economic benefits or utility

Usage of the bridge, and therefore its utility, will depend on the pricing of the toll.

This is so because the toll will eliminate a certain number of potential customers. Since this will make no change to the operating expenses for the bridge, there will be a diminution in the surplus, and this diminution will increase as the level of the toll rises. In options 1 and 6, no actual toll is envisaged, and consequently the use of the bridge – and therefore its utility – is maximised. In the other options, the traffic will be less and there will therefore be a lesser overall surplus.

Utility has been estimated using a conventional supply & demand curve. To make the computations easier, we will not use a constant elasticity curve but one in which the elasticity for traffic “T” in relation to the generalised cost is a linear function of generalised cost “C”. Such an approximation provides a satisfactory representation of the behaviour of users/customers. The coefficient of elasticity (∆T/T)/(∆C/C) applied here has the form C/Co, in which Co is the optimum revenue (see graph no. 4)

The equation defining traffic as a function of generalised cost is therefore: T=To*e^(-C/Co).

The starting point prior to the construction of the bridge is represented by point A, for which the coordinates are Ci (€15.00 generalised cost) and Ti (10,000 vehicles per day). In the pages which follow, we vary the elasticity of the traffic in relation to the generalised cost, while of course leaving the starting point unchanged, since this represents the current situation. Elasticity will thus be varied over the range – 0.42 to – 1.27, with the highest elasticity in absolute value corresponding to frequent, short-distance traffic.

If the constructed facility were free of charge, the final situation would be represented by point C, for which the coordinates are Cg for generalised cost estimated at €1.00 and Tg, which corresponds to traffic of 27,000 vehicles per day. A €9.00 toll raises this generalised cost to €10.00 of course (point B, for which the coordinates are Cp – €10.00 – and Tp, the figure for which is 15,000 vehicles/day). Although this price is acceptable for journeys over middling distances, it is too high for short trips, which should, for specific and very frequent users, be set preferably in the region of €4.00, which would raise the generalised cost to €5.00.

The economic surplus for users is represented by the area described by (Ci-A-B-Cp), the total surplus by the area (Ci-A-B-D-Cg), and the amount of revenue by the area (Cp-B-D-Cg). In order to carry out the economic calculations, we have assumed the surplus to be constant over time, which is pessimistic given that demand on the one hand, and, on the other, the willingness to pay in terms of hourly traffic, will increase as the years go by, but this is offset by the fact that we have neglected to include the costs of maintaining and operating the infrastructure, an amount equal to some 15% of total revenue.

Depending on the option chosen for the construction of the bridge, there may or may not be a toll charge. The level of this charge is calculated on the basis of the sum required to repay borrowing and provide a return on capital. For each level of toll charge, there is a level of revenue and an economic surplus.

 

 

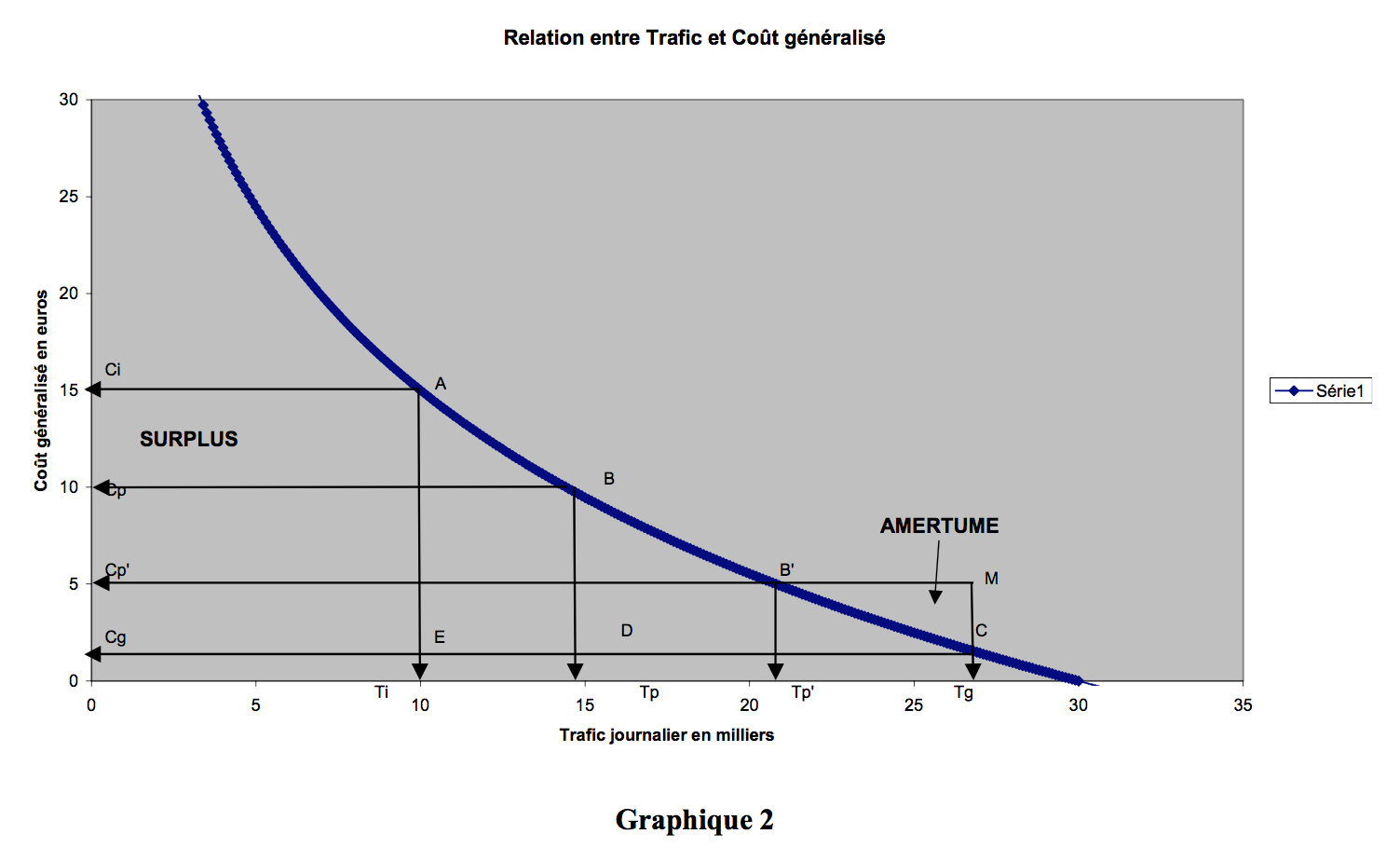
The maximum level of charge acceptable in political terms to frequent users (see our previous articles) is midway between Ci and Cg, or half of (15-1), i.e. €7.00. In our example, we have chosen a charge of €4.00, which yields a generalised cost of €5.00. Political acceptability is illustrated by the area representing bitterness (M-C-B’), which must be compared with the total amount of toll revenue (the rectangle Cp’-B’-D’-Cg) and with the corresponding surplus (Ci-A-B’Cp’).

The total cost of the construction

If the public funds devoted to the construction of the bridge come solely from the State budget, the contracts for the engineering studies, the building of the bridge and the operations of it will be entered in the accounts on the basis of the usual procedures when the State is the owner of the project. If the chosen contractual arrangement provides for a broader delegation of responsibility to private enterprise (under a concession agreement or a public-private partnership), the overall cost of the construction will not be the same. Remember that total cost comprises the following:
costs relating to upstream phases such as project programming, preliminary studies, preliminary project design and building the public tender dossier, in addition to awarding and signing the contracts ;
construction costs (detailed engineering studies, the construction work per se, including possible adverse claims and insurance costs) ;
Generalised Cost (euros)
the costs of maintaining and operating the structure throughout its life cycle ;
the costs of risks.
A number of specialists in the field (NAO 8, CSTB 9, MIQCP 10) have arrived at the conclusion that the public-sector process costs significantly more than the private-sector process associated with a concession agreement or a public-private partnership. There are two categories of reasons for this: purely technical considerations relating to the efficiency of private enterprise compared with public bodies, and considerations relating to budgetary considerations.

It is impossible to give precise figures contract by contract for the gains made when the overall process is entrusted to the private sector compared with the conventional procedure followed when the project is wholly owned by the State. This is because the parameters vary from one contract to the next. A public project owner which does a great deal of construction work will have technical skills comparable with those of a large coronation, in addition to effective budget planning. Such a body will know how to stand up to unnecessary demands generated by political lobbying and will avoid wasting public funds. But it is often the case that project owners are insufficiently experienced, and budgetary regulations may delay the entry into service of a structure that is almost finished because a section of highway or minor infrastructure required to finish the operational portion of the network are lacking. We should cast our minds back to the examples of the two viaducts close to the Millau viaduct, which have had to wait for nearly four years to be commissioned after the termination of the construction work. This adds 25% to their economic cost.

Generally speaking, European decision-makers consider that total delegation to private enterprise, which shoulders the risks involved in design-construction-maintenance and keeps to project deadlines, will reduce the total cost of the production process for the final structure by about 17%, and provide a time saving of 10% compared with the public-sector process. If we combine these two factors, we arrive at a gain of 20% in our bridge example.

In the case of publicly-owned corporations, a SEMCA for example [Société d’économie mixte concessionnaire d’autoroutes / public-private motorway concession holder] or an EPIC [Établissement public industriel et commercial / public industrial or commercial establishment], there is less budgetary constraint and the specialist nature of such bodies usually means that they have a good level of competence. Consequently, in our comparison of the options, we have considered that the difference in total cost between private enterprise and an EPIC is no more than 10%.

The cost of private and public capital

The introduction of private enterprise into the funding of construction is reflected in an increase in financial expenses because the borrowing of the private partner will be at higher interest rates than its public-sector principal. The precise rate will depend on two parameters:
the base rate for long-term government borrowing, which derives from the combination of decisions by public authorities and the confidence felt by the banking sector in the robustness of the national economy ;
the way the total risk is split between the private and public sectors, which in turn defines the spread between interest rates for the public and private sectors.
8 9
10 MIQC: Mission Interministérielle pour la Qualité des Constructions Publiques / interministerial mission for quality in public building.
NAO : National Audit Office, the UK equivalent of the French Cour de Comptes
CSTB: Centre Scientifique et Technique du Bâtiment / scientific and technical centre for the construction industry
9

In our example we have chosen to apply a figure of 5.7% per year in real terms (not including inflation) for the rate representing the cost of private finance. This rate relates to an approach to project financing in which the entirety of the traffic risk is borne by the private-sector partner. This a figure for WACC (Weighted Average Cost of Capital), which combines a return on private capital and a loan interest rate, the rate of the former being significantly higher than the latter, but applicable to a smaller part of the capital actually raised.

Where the construction is funded out of public funds through a SEMCA or an EPIC, we have considered that over the long term that the cost of the finance is less but the public shareholder wishes nevertheless to receive dividends. We have chosen to apply a rate of 4.2%.

If the construction is financed solely out of public funds, we nevertheless considered in pricing the toll charge that the capital will have come at a cost, set at 3.2%, this figure being equal to the rate in real terms on finance from the public authorities. This means that the final cost accounting balance for the bridge would be nil, with no profit or loss.

Revenue generated by the utility of the construction

An economically viable construction will generate activity and therefore fund flows. Such flows will be split between the private-sector actors, commercial or industrial companies, and the public-sector actors. Recent research, notably that directed by Professor Rémy Prud’homme at the University of Paris 12, have shown it to be possible to estimate budget revenue for the State, which collects taxes and social contributions, at 20% of the annual surplus. In the case of local government this percentage falls to approximately 3%. Given the importance of the construction to the national economy, it is the situation of the State that we look at here.

The results

Politically acceptable pricing

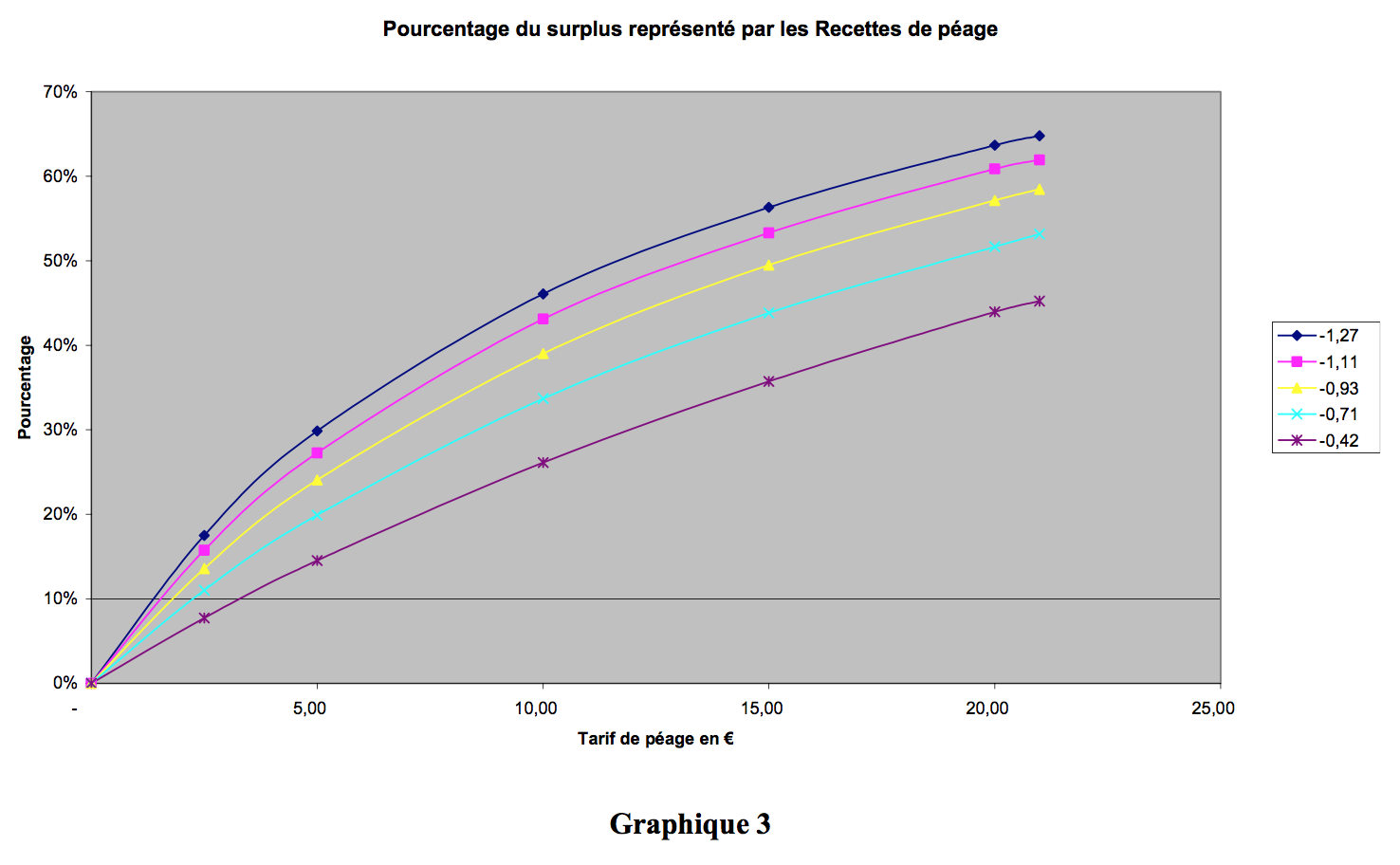
In previous articles we have put forward the political concept of “bitterness” in order to illustrate the problem raised by frequent users of infrastructures in urban areas for which tolls are charged. In fact, it is possible to define a rational approach to this illustration by examining the percentage contribution of toll revenue to the total surplus generated by the facility.

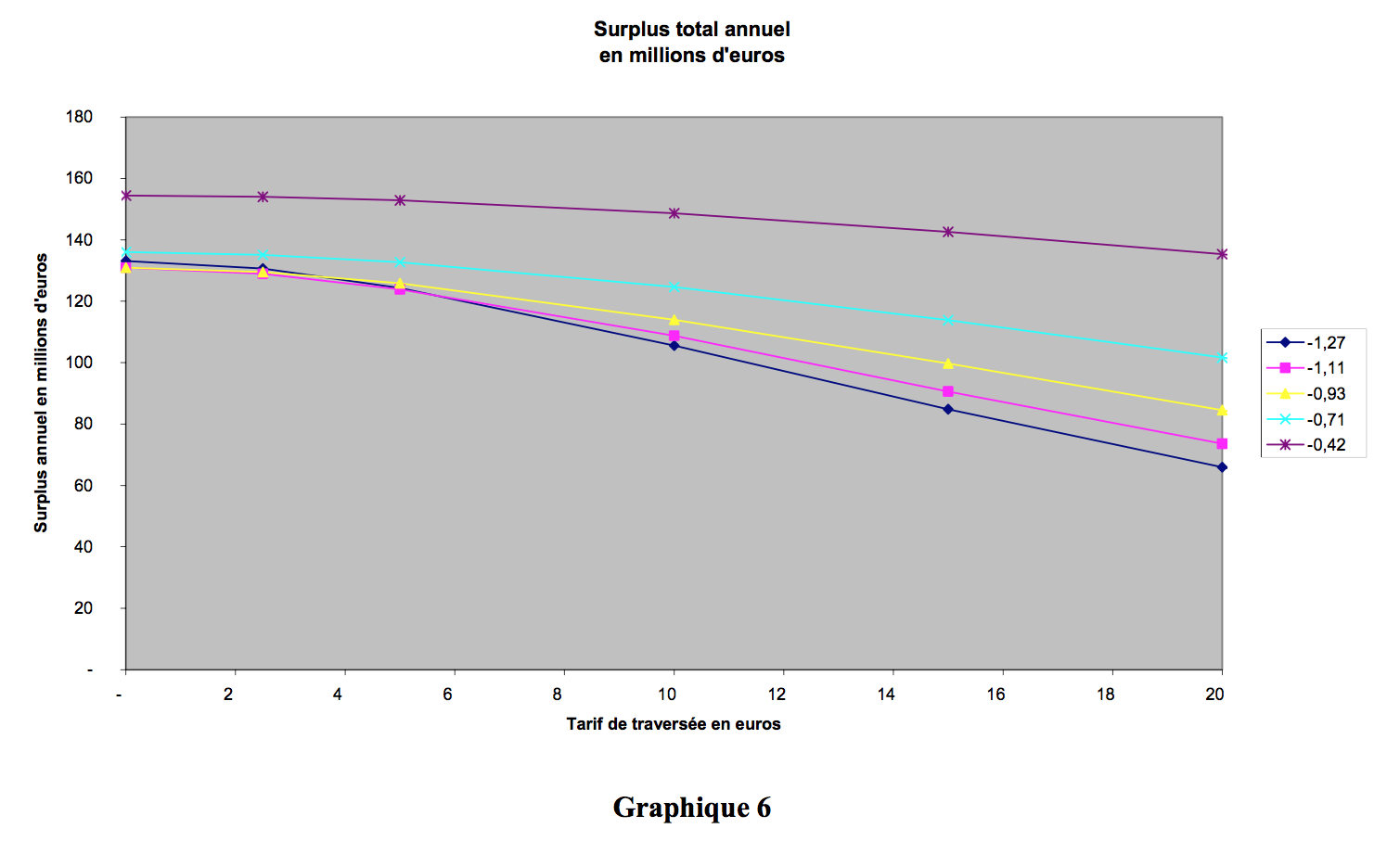
The set of curves shown below (graph 5) depicts the share of toll revenue in the total surplus generated. It is clear that if this share is too substantial, there will be a political backlash. Frequent short journeys, which correspond to a limited willingness to pay, present the greatest elasticity in absolute value (-1,27). For a toll of €9.00, over 40% of the surplus is generated by the toll charge: it is hardly likely that potential frequent users of the bridge will agree to this. It is for this reason that a price around €5.00 would be more suitable for them. Conversely, for users for whom elasticity is limited, a much higher price is acceptable, with a toll of €12.00 corresponding to a levy in revenue form equal to only 30% of the total surplus generated.

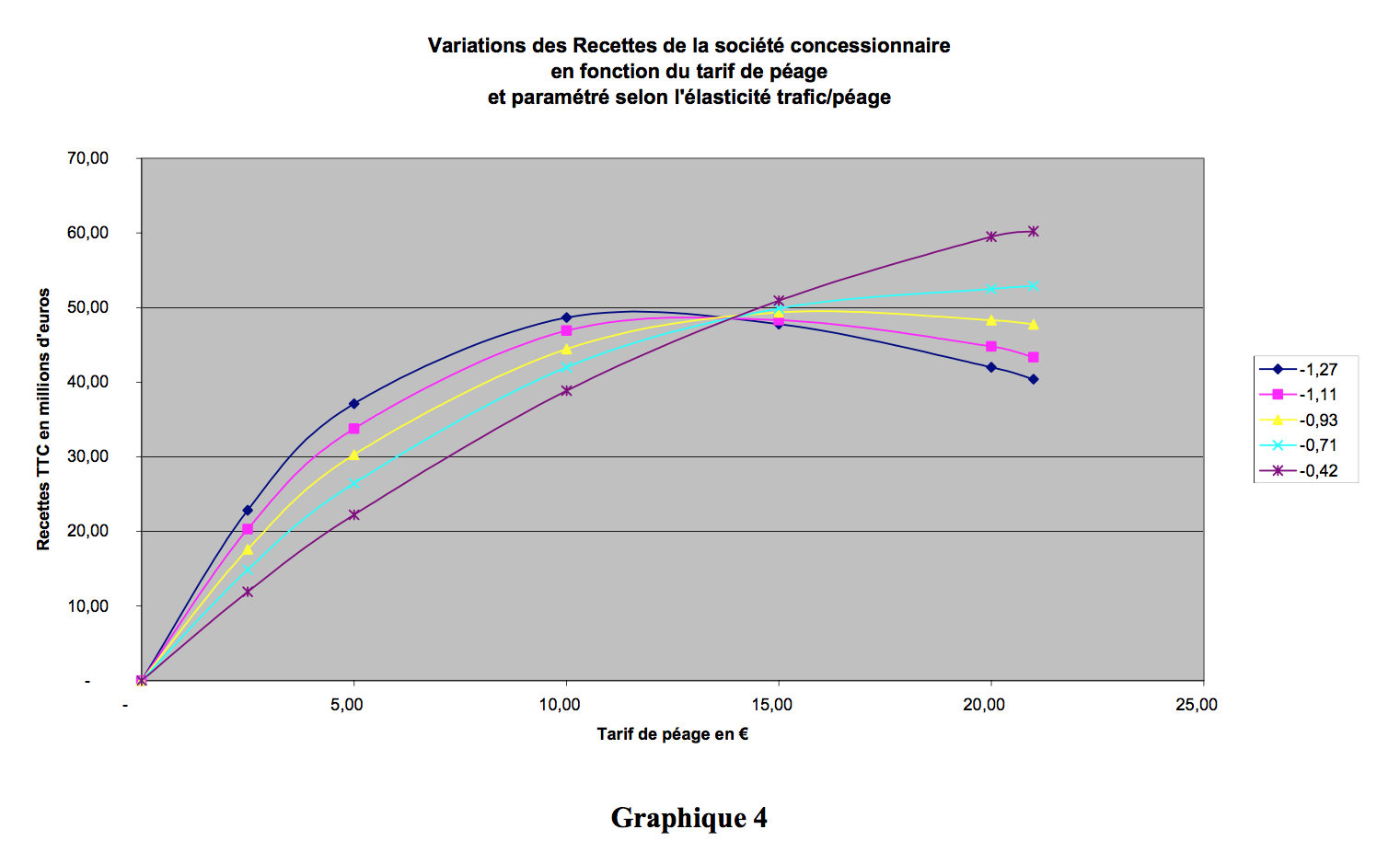
We can in fact see in graph 6 below, which represents variation in revenue as a function of toll price and elasticity, that high elasticity of – 1.27 produces a curve giving a maximum for revenue around €10.00, while low elasticity leads to a maximum which falls outside the practical scope of our example.

For the different project structures we analyse later, we have always applied a rate of €9.00.
80,00 70,00 60,00 50,00 40,00 30,00 20,00 10,00 –
Variation of revenue for the concession holder against toll level
and adjusted to reflect traffic/toll elasticity

 

 

Economic scorecards for the different options

First of all, we should look at the total annual surplus (graph 7). For an investment of €700m, the annual surplus with a zero toll is in the region of €135m, which provides a very good return in socio-economic terms and entirely justifies the construction project and the finance contributed to it.

Naturally, the higher the toll the smaller the economic surplus. Up to €5.00, the loss in economic surplus is limited, but above this level it begins to rise, doing so increasingly steeply as absolute value elasticity rises.

The point at €20.00 is entirely theoretical given that it is difficult to imagine that the generalised cost can be higher after the opening of the bridge than it was before. This extreme case can indeed occur in the case of city centre improvements undertaken to reduce car traffic, but the latter relate to town planning projects rather than transport infrastructure.

Table 1 below contains an economic scorecard for the various options described above. It should be remembered that economic NPV is calculated using a discount rate of 6%.

The most desirable situation from the economic standpoint is the shadow toll or PPP arrangement. The worst is to charge a toll for an infrastructure which has in the end been financed from public funds. The postponing of a project does not affect its economic viability, at least if our hypotheses hold true, but it does diminish its economic interest. The ranking by economic NPV is very close to a ranking by IRR, but the two lists are nevertheless not identical: it is the NPV ranking which seems most relevant to us.

The financial scorecard for the different options

The result of this ranking is in this case quite different (table 2): the project structure involving a toll will impose least constraints, and may even be the most profitable for the Ministry of Finance’s budget.

Options 4, 5 and 2 are fairly similar and it is problematic to derive from them any general rule as to effectiveness. However, we do find in the results already examined in our previous articles that option 5 is very efficient (bridges over the Tagus in Lisbon), and better than the SEMCA solution or projects for which a rather high tariff shifts the result away from the economic optimum. We certainly see reflected here the confused debates on the total or partial privatisation of such facilities, an issue which is of concern to many countries in Europe and Latin America at the present time. In fact, to give a clear answer on the choice to be made, what is necessary is not to think in terms of a constant surplus over time, but to introduce real-life parameters to match the technical and financial position of the country concerned. If this is done, the answers will vary case by case.

We can also see that the shadow-toll solution is very expensive for the public purse, but is nevertheless better than solutions which make exclusive use of public funds taken from budget. As for the reduction in budgetary cost linked to a delay in launching the construction work, this is a mechanism that is so familiar that there is hardly any need to dwell upon it: doing nothing is always less expensive than actually doing something.

It is worth pointing out that the transfer of risk to the private sector is a factor, although not a key factor, in the calculations. This is so because if we assume that the public authorities retain the risks that they are best able to bear, that is to say traffic risk, financial institutions will reduce the cost of the debt and the toll level can then be reduced, which will in turn increase the socio-economic benefit of the resulting facility.

By reducing the WACC for the private sector to 4.6% in real terms instead of 5.7%, it can be seen that the ranking of the different project structures changes significantly.

From the economic point of view (table 3), it is obvious that the private-sector project structures move up the list:

 

Seen from the budgetary point of view, the ranking changes (table 4): option 2 moves up to first place, and option 5 slips from first to second position, although the difference is fairly small. Option 4 lags noticeably behind the two leaders.

Options 2, 5 and 4 correspond respectively to the recent Millau viaduct and A28 projects and traditional SEMCA-type projects. Good IRRs and good NPVs, good formulas for the Ministry of Finance, these are all satisfactory solutions.

However, the most profitable investments are to be made at the present time in the suburbs and surrounding areas of the major regional conurbations in order to resolve the most flagrant network overload problems. Whether decision-makers apply real tolls or not, public funds will be needed. And in that case, a process based on a comprehensive public-private partnership agreement can provide a good technical solution to the need to raise capital.

Conclusion: a plurality of solutions

The study presented above makes use of conventional economic methods familiar to professionals. The use of a concrete example such as the Rion-Antirion bridge brings into sharp focus the applicable mechanisms in determining the level of the toll and drawing up an overall economic balance sheet.

It can be seen that there is no single, systematic solution to a practical issue involving the construction of a given infrastructure in a given human and geographical environment. In the light of this plurality of options, it is the task of the decision-makers to undertake fine-grained analysis of the overall context in economic, legal, budgetary, financial and other terms, and of the constraints that flow therefrom, before pronouncing on the optimum solution for the circumstances. Specifically, estimation of utility is a delicate task, since while utility can include factors that are easily measured in terms of time savings, there are also others, relating to sociological considerations or human geography, that are less straightforward.

However, one fact is invariably to be seen in every case: there are no miraculous financial solutions that can make a construction economically viable if its socio-economic fundamentals are not right.

Some observations on France

State debt and public departments

In France today, the constraint imposed by debt is particularly stringent. The psychological barrier at €1,000bn was recently breached. The stability programme 11 for the period 2005-2007 presents the balances of the public departments and agencies and forecasts for debt on the basis of two growth scenarios: annual growth of 2.5% or 3%. Unfortunately, there is little likelihood that this can actually come about and the hypothesis of a stable growth trajectory over the long term at 2.5% from 2005 onwards, which would enable inroads to be made in the debt/GDP ratio from 2006 on, remains an optimistic one.

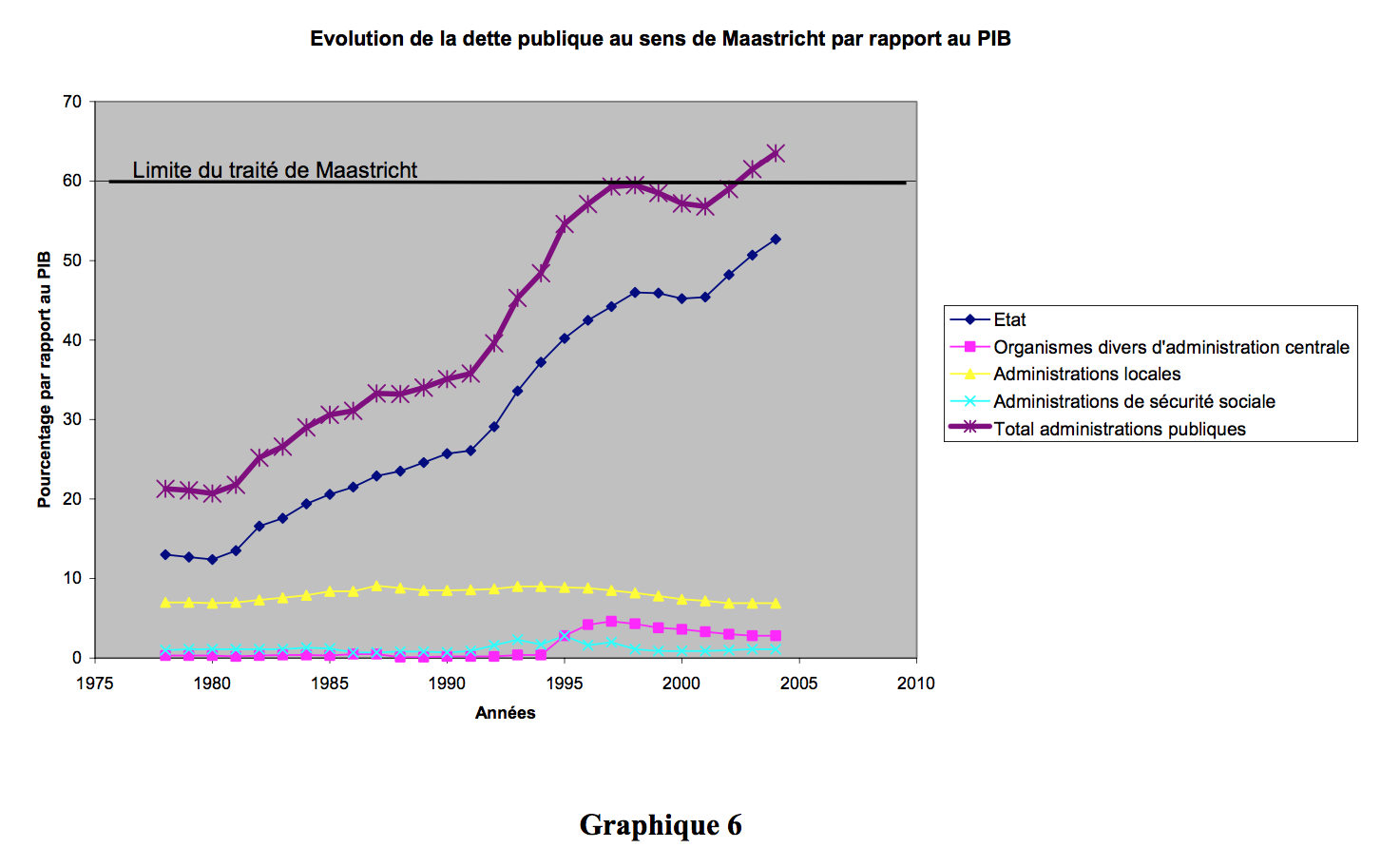
Bearing in mind that the much-discussed debt/GDP ratio under the Treaty of Maastricht is set at 60%, we can see in the following graph that the situation in France will require efforts to be made to achieve efficiency and rigour throughout the public sphere for several years if the country is to get back within the defined standards.

Evolution de la dette publique au sens de Maastricht par rapport au PIB
Limite du traité de Maastricht
Années
Changing levels of public debt as defined by Maastricht in relation to GDP Limit defined by Treaty of Maastricht
Percentage of GDP
Years

State
Sundry central government bodies Local authorities
Social security bodies
Total for public sector bodies

Source: MINEFI

What is apparent here is a high level of expansion in debt during a period of low growth in GDP, along with a limited reduction in that debt during a period of strong growth in GDP. We are in a period of low interest rates, which has the effect of lightening the debt burden, but we should not forget that public debt is a deferred tax charge, which future generations will have to repay.

Lastly, in the road transport domain, the real issue with regard to project structures can be summed up in two points:
16
Etat

Organismes divers d’administration centrale

Administrations locales

Administrations de sécurité sociale

Total administrations publiques
Pourcentage par rapport au PIB
Correct evaluation of the political acceptability of the toll and the associated elasticity, designing pricing structures that are a little less basic than what we currently have in Europe in the road transport sector, by for example seeking solutions more similar to those implemented by professionals in the air and rail transport sectors ;
Correct and comprehensive evaluation of the benefits of a construction over its entire life cycle, including the revenue generated and operating costs, plus the socio-economic benefits produced, going further than a simple computation of the time saved by road users.
We might suggest to the reader what we ourselves have done, that is to go back to the broad principles set out by Adam Smith and Jules Dupuit, but, on a more topical note, we will conclude by quoting once again a former French national planning commissioner, Hervé Guaino, who recently wrote the following in a newspaper column:

“It is the quality of investments that will determine [our] standard of living and not how those investments are funded. To express this another way: our sole focus should be not the measurement of the indebtedness of yesterday, but rather reflection on what might be the most judicious investments to prepare for the growth of tomorrow.”